
In the above diagram, translation (glide) performed on the foot, and then reflection across the parallel line of translation, then again glide followed by the refection, this foot steps are the typical example of glide reflection. In everyday life, a classic example of glide reflection is the track of footprints left in the sand by a person walking over it.
Reflection and glide reflection are opposite isometry. From the four types of transformations translation, reflection, glide reflection, and rotation. Distance remains preserved but orientation (or order) changes in a glide reflection. Reflection transformation is an opposite isometry, and therefore every glide reflection is also an opposite isometry. Look at our example of this concept below.Īn opposite isometry preserves the distance but orientation changes, from clockwise to anti-clockwise (counter clockwise) or from anti-clockwise(counter clockwise) to clockwise. Whether you perform translation first and followed by reflection or you perform reflection first and followed by translation, outcome remains same.įor example, foot prints. Outcome will not affect if you reverse the composition of transformation performed on the figure. Commutative properties:Ī glide refection is commutative. Glide reflection occurs when you perform translation (glide) on a figure and followed by a reflection across a line parallel to the direction of translation.
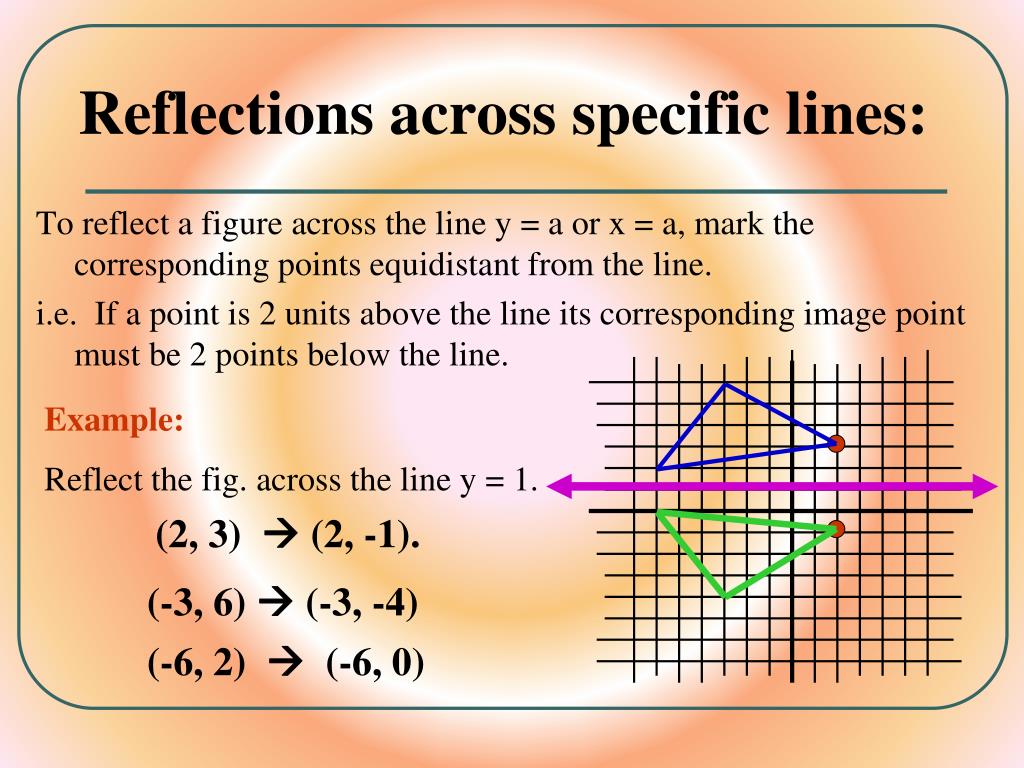
Glide reflections are essential to an analysis of symmetries. A glide reflection is – commutative and have opposite isometry. Glide reflection is the composition of translation and a reflection, where the translation is parallel to the line of reflection or reflection in line parallel to the direction of translation. Every point is the same distance from the central line after performing reflection on an object.

Reflection means reflecting an image over a mirror line. Translation simply means moving, every point of the shape must move the same distance, and in the same direction. Therefore, Glide reflection is also known as trans-flection.

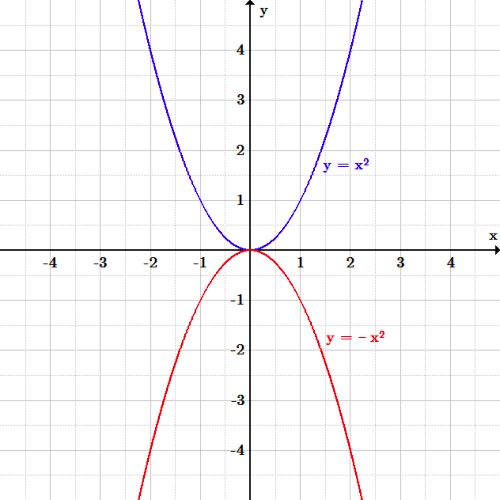
First, a translation is performed on the figure, and then it is reflected over a line. The reflection of a point $(x,y)$ over the x-axis will be represented as $(x,-y)$.Īllan was working as an architect engineer on a construction site and he just realized that the function $y = 3x^+4(-x) -1)$.Definition: A glide reflection in math is a combination of transformations in 2-dimensional geometry. In that case, the reflection over the x-axis equation for the given function will be written as $y = -f(x)$, and here you can see that all the values of “$y$” will have an opposite sign as compared to the original function. When we have to reflect a function over the x-axis, the points of the x coordinates will remain the same while we will change the signs of all the coordinates of the y-axis.įor example, suppose we have to reflect the given function $y = f(x)$ around the x-axis.
#Reflection on y axis equation how to
How To Reflect a Function Over the X-axis


 0 kommentar(er)
0 kommentar(er)
